Section 4.6: Applications to Business

By the end of this section, the student should be able to:

• Solve consumer and producer surplus problems.
• Solve continuous income stream problems.

Consumer and Producer Surplus

Here is a demand and supply curve for a product. Which is which?

The demand curve is decreasing. Lower prices are associated with higher quantities demanded; higher prices are associated with lower quantities demanded. Demand curves are often shown as if they were linear, but there’s no reason they have to be.

The supply curve is increasing. Lower prices are associated with lower supply, and higher prices are associated with higher quantities supplied.

The point where the demand and supply curves cross is called the equilibrium point [latex](q^*, p^*)[/latex].

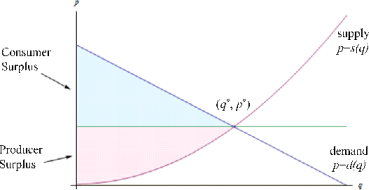
Suppose that the price is set at the equilibrium price so that the quantity demanded equals the quantity supplied. Now think about the folks who are represented on the left of the equilibrium point. The consumers on the left would have been willing to pay a higher price than they ended up having to pay, so the equilibrium price saved them money. On the other hand, the producers represented on the left would have been willing to supply these goods for a lower price – they made more money than they expected to. Both of these groups ended up with extra cash in their pockets!

Graphically, the amount of extra money that ended up in consumers’ pockets is the area between the demand curve and the horizontal line at [latex]p^*[/latex]. This is the difference in price, summed up over all the consumers who spent less than they expected to – a definite integral. Notice that since the area under the horizontal line is a rectangle, we can simplify the area integral: [latex]\int\limits_0^ \left( d(q)-p^*\right)\, dq = \int\limits_0^ d(q)\, dq – \int\limits_0^ p^*\, dq = \int\limits_0^ d(q)\, dq – p^*q^*.[/latex]

The amount of extra money that ended up in producers’ pockets is the area between the supply curve and the horizontal line at [latex]p^*[/latex]. This is the difference in price, summed up over all the producers who received more than they expected to. Similar to consumer surplus, this integral can be simplified: [latex]\int\limits_0^ \left( p^*-s(q) \right)\, dq = \int\limits_0^ p^*\, dq - \int\limits_0^ s(q)\, dq = p^*q^* - \int\limits_0^ s(q)\, dq.[/latex]

Consumer and Producer Surplus

Given a demand function [latex]p = d(q)[/latex] and a supply function [latex]p = s(q)[/latex], and the equilibrium point [latex](q^*, p^*)[/latex]:

• The consumer surplus is [latex]\int\limits_0^ d(q)\, dq – p^*q^*.[/latex]
• The producer surplus is [latex]p^*q^* - \int\limits_0^ s(q)\, dq.[/latex]
• The sum of the consumer surplus and producer surplus is the total gains from trade.

What are the units of consumer and producer surplus? The units are (price per item)(quantity of items) = money!